accueil
these
sommaire
Ultrasons : Traducteurs
 
 

Génération et propagation ultrasonore appliquée au CND

Retournez à : 1. Introduction - 2. Ondes élastiques - 2.2 Équation de propagation...
Allez à : 4. Contrôle Non Destructif par ultrasons - 5. Bibliographie
Plan du site...
 
Plan du chapitre 3 - "Traducteurs ultrasonores" :
3 - Traducteurs ultrasonores
3.1 - Le phénomène piézoélectrique
3.1a - Propriétés de céramiques piézoélectrique
3.1b - Le couplage électromécanique
3.2 - Génération des ondes ultrasonores
3.2a - Traducteur ultrasonore
3.2b - Modélisation d'un transducteur à ultrasons
3.3 - Matériaux piézocomposites
3.4 - Caractéristiques du rayonnement des traducteurs à ultrasons
3.4a - Traducteurs plans
3.4b - Traducteurs focalisés
3.5 - Traducteurs multiéléments
3.5a - Balayage électronique par commutation
3.5b - Balayage sectoriel et volumique
3.5c - Retournement temporel
   
   
   

3 -Traducteurs ultrasonores

  
Les ondes ultrasonores atteignent des fréquences supérieures à la gamme audible qui s'étend de 20Hz à 20kHz. En imagerie médicale comme en CND, on utilise des fréquences généralement comprises entre 0.5 et 20MHz, ce qui implique l'utilisation de procédés spécifiques pour réaliser des émetteurs-récepteurs ultrasonores.  
 

3.1 - Le phénomène piézoélectrique

  
 

3.1a - Propriétés de céramiques piézoélectriques

  

Un solide est dit piézoélectrique s'il se polarise électriquement sous l'action d'une contrainte (effet direct) et se déforme si un champ électrique lui est appliqué (effet inverse). Pour cela on utilise le phénomène mis en évidence par Pierre et Jacques Curie [4] qui est la conséquence d'un couplage entre les propriétés mécaniques et électriques d'un matériau piézoélectrique. On peut décrire des équations d'état piézoélectrique, reliant des grandeurs mécaniques comme la déformation $ S$ et la contrainte T, à des grandeurs électriques comme l'induction $ D$ et le champ électrique $ E$ [2,3]:

(...)

(20)

où $ c$ le tenseur des constantes élastiques (en Pa), $ s$ le tenseur des raideurs élastiques (inverse de $ c$), $ \varepsilon$ la constante diélectrique (en F/m) et $ \beta$ inverse de $ \varepsilon$. La transposée de la matrice $ X$ est notée $ X^t$ et $ X^Y$ indique que $ X$ est considéré à $ Y$ constant ou nul. Nous trouvons aussi dans les équations (20) d'autres constantes représentatives du couplage piézoélectrique :
- La constante de charge $ d$ traduisant la proportionnalité entre la contrainte et l'induction à champ électrique nul ou constant (en C/N).
- La constante de tension $ g$ traduisant la proportionnalité entre la contrainte et le champ électrique à induction nulle ou constante (en V.m/N).
- La constante piézoélectrique $ e$ traduisant la proportionnalité entre la déformation et l'induction à champ électrique nul ou contant (en C/m$ ^2$).
- La constante piézoélectrique $ h$ traduisant la proportionnalité entre la déformation et le champ électrique à induction nulle ou constante (en V/m).

Les équations (20) combinent les équations issues des lois mécaniques de Hooke (16) aux lois de Maxwell, suivant les conditions aux limites imposées sur un échantillon.

Les matériaux ayant de telles propriétés sont de cristaux comme le Quartz (SiO$ _2$), le Niobate de Lithium (LiNbO$ _3$) ou le Tantalate de Lithium (LiTaO$ _3$). Pour des applications médicales ou pour le CND l'utilisation de céramiques polycristallines est plus courante. Par exemple, le PZT composé de plomb, de zirconium et de titane, est fabriqué par frittage de microcristaux à haute température en présence d'un fort champ électrique statique d'environ 20kV/cm. Par convention, ce champ est orienté suivant l'axe $ \vec{z}$, considéré comme un axe de symétrie de révolution. Cependant ces céramiques ont quelques contraintes d'usage notamment en température. La température de Curie, qui se situe selon le type de céramique entre 200 et 400°C, fixe la limite au dessus de laquelle la polarisation permanente, donc la piézoélectricité, disparaît :

Bas
 
Tableau 1: Caractéristiques électromécaniques de matériaux piézoélectriques [5]. La permittivité diélectrique dans le vide est $ \varepsilon _0=8,854.10^{-12}$ F/m.
Matériau piézoélectrique $ \rho ~ (.10^3$ kg.m$ ^{-3})$ $ v_L$ (m/s) $ \varepsilon_{33}^S/\varepsilon_0$
       
       
LiNbO$ _3$ coupe $ \vec{z}$
4.7
7316
39
Céramique P1-94
7,9
4273
2230
       

Le tableau 1 montre quelques constantes caractéristiques d'une céramique du type PZT par rapport à un cristal. La céramique est plus lourde et a une célérité, pour les ondes de compression, plus faible que pour le cristal, qui est de fait un bon résonateur mécanique. Le principal avantage de la céramique est dans sa forte permittivité diélectrique, représentée par le tenseur $ \varepsilon$ liant le champ électrique $ E$ à l'induction $ D$. En particulier sa composante $ \varepsilon_{33}^S$ :

Bas

Haut
$\displaystyle D_3=\varepsilon_{33}^S E_3$
 (21)

Dans la suite, nous verrons qu'il est possible de caractériser le rendement d'un tel dispositif qui consomme de l'énergie électrique pour fournir de l'énergie mécanique. 		 

3.1b - Le couplage électromécanique

 

Le couplage électromécanique est la faculté d'un matériau piézoélectrique à convertir de l'énergie électrique en énergie mécanique. Il est caractérisé par le coefficient noté $ k$ :

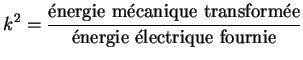$\displaystyle k^2=\frac{\text{\'energie m\'ecanique transform\'ee}}{\text{\'energie \'electrique fournie}}$
 (22)

L'expression de $ k$ dépend en fait de la forme de la céramique et de son mode de vibration. Pour une plaque suffisamment fine suivant l'axe 3 vibrant en épaisseur, le coefficient électromécanique est caractérisé par $ k_t$ (t comme thickness) ; $ k_{31}$ pour une plaque suffisamment fine suivant l'axe 3 vibrant en cisaillement suivant l'axe 1 ; $ k_{33}$ pour un barreau de rayon fin suivant l'axe 3 vibrant en compression suivant l'axe 3. La figure 2 donne l'expression de ces coefficients d'après le standard de l'IEEE [6].

\begin{figure}\centering %% \input{figs/sch_k_t_33_31.eepic} \end{figure}
Figure 2 : Coefficients de couplage électromécanique [6]. Les éprouvettes sont polarisées suivant l'axe 3.
  
Le coefficient $ k_t$ est particulièrement approprié pour caractériser des céramiques qui composent les transducteurs fonctionnant en mode épaisseur, généralement utilisés pour des traducteurs à ondes L. En CND des céramiques de type PZT sont les plus employées car elles ont un coefficient de couplage $ k_t$ relativement élevé, permettant une bonne conversion du signal électrique en vibration acoustique.  
   
 
Haut
 

Page Précédente - Equation de propagation... (suite) - Page suivante - Génération des ondes...
Retournez à : Introduction - Ondes élastiques
Allez à : Rayonnement des traducteurs - Traducteurs multitéléments
 
Imprimer la page
Télécharger le chapitre
 
milieu solide
génération des ondes